Reflecting over my years of teaching, I have found that students are challenged by what would seem to be an easy question – “How do we convert from one unit of measure to another?” When confronted with this type of question, I have come to recognize that many students fall back on relying on a procedure that they try to recall. For example, when asked how many feet 15 yards is equal to many students seem to begin contemplating in their mind “Do I multiply or divide by 3?”. Since they have had many problems of this sort over their mathematical career, are quite familiar with the units of measure, and have enough number sense to realize the answer should be bigger, they generally do see the need to multiply by 3 and arrive at the correct answer of 45 feet. The obstacle to this problem solving process, however, is that it is not very robust. It will not guarantee them success when they are asked to convert units they are not as familiar with such as in mole conversion in Chemistry or converting area or volume units. I contend that there is a much better option.
As a mathematics educator, we have a powerful way of thinking that can be used in all unit conversions. We need to make it very clear to students that when we convert from one unit of measure to another we are NOT changing the length, area, volume, speed, or quantity of the item under consideration but are simply using another unit of measure to describe it. For example, when we convert 15 yards of rope into feet we are NOT lengthening or shortening the amount of rope. Therefore, we will be multiplying the measurement by a factor of 1 so that we do not increase or decrease the quantity of rope. In other words,

We would NOT get the same amount of rope if we multiplied by any other amount other than 1 such as 2.

Therefore when we convert from one unit of measure to another we need to choose the unit of one that will allow us to convert to the appropriate unit we hope to achieve. The following conversion from yards to feet technically WILL give us the same quantity of rope we had initially because we are multiplying by a factor of 1. However, we do not get the unit of measure we hope for.

We need to choose the unit of one that will do the proper conversion. Let’s try again.

This is incorrect too. With one more try, we see the result in the unit of feet.

The idea of multiplying by a unit of one is very powerful. If we use an example of converting area units we see how the notion can be applied in another context. Assume we are asked to convert 2 square miles (mi2) to square feet (ft2) and we apply this way of thinking. Notice that since there are two mile units multiplied together we have to convert each unit of measure to feet.

Likewise, this can be done with measurements of volume involving cubic units of measure too. Rather than looking at an example of volume however let’s try converting imaginary units of measure to demonstrate how this way of thinking can be used even if we don’t understand what the units of measure are actually quantifying. Given the following equivalent units of measure do the conversion.

For one final example, let’s take a look at a typical Chemistry problem involving unit conversion.
How many moles are in 25 grams of water? We are given that 1 mole of water contains 18 grams of water. We do the calculation.

Returning once more to the problem of converting 15 yards to feet, another equally powerful way of thinking is to envision 1 yard as 3 one foot units (or 1 yard = 3 feet). That is, every yard has 3 copies of 1 foot length segments of rope. So, 1 foot is 1/3 times as large as 1 yard or 1 yard is 3 times as large as 1 foot. Therefore, 15 yards is times as large as 1 foot or 45 times as large as 1 foot equaling 45 feet.
A visualization for the problem “convert 15 yards to feet”, we might think like this…imagine that the line segment has a length of 15 yards.

We can think of cutting this into 15 pieces of equal length.

Since we cut the length of 15 yards into 15 equal parts, each segment is 1 yard and each of those yards has 3 feet within it.

In this way of thinking, multiplicative reasoning is at the heart of the explanation. Combining this multiplicative/proportional reasoning with a deep understanding of unit conversion creates a more robust understanding that not only serves to help with unit conversion but will help with the big idea of proportional or multiplicative thinking.
In conclusion, as is the case with much of mathematics if we can expose for students powerful ways of thinking then they will have tools they can use in multiple contexts and academic disciplines. If we teach students the concept of the unit of one and the notion that when converting units of measure we are not changing the quantity of an object, students will be well served.
Trey
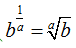 Let’s first take a look at
Let’s first take a look at 












