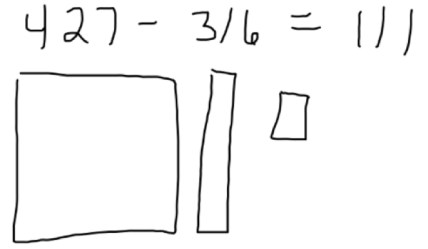Misunderstanding the Common Core – Part II

I say Part II fully expecting that there may be Parts III, IV…LVI…coming just like the Super Bowl! There is much misunderstanding and bashing that is not justified when considering the actual content and practice standards.

Consider an image that is going around Facebook:

Misunderstanding #1: This is NOT an example of common core somehow promoting some new, “ridiculous” way to perform subtraction. In fact, a big part of the common core in the elementary grades is computational fluency. That is, students absolutely should be expected to subtract the problem presented here in “under 5 seconds”!  To say otherwise shows a complete ignorance of the common core standards. Go read the standards and their supporting documents and then feel free to engage in a dialogue about how they can be improved.

Standards – http://www.corestandards.org/Math/

Progressions – http://ime.math.arizona.edu/progressions/

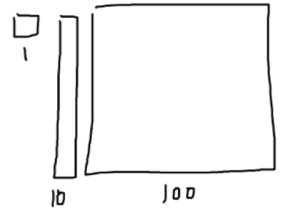
Misunderstanding #2:  Many of the Facebook comments to the image are of the form, “yea…why not just show the kids how to do the problem in under 5 seconds??!!!?” As stated earlier, computational fluency is the goal…but how do kids get there? They get there when they are able to think about the problem, make sense of the situation, engage in methods that make sense and are grounded in foundational mathematical thinking such as place value and the meaning of subtraction. Developmentally, 2^nd graders are not ready to just jump into the formal, traditional algorithm. To deeply understand how to subtract, students are encouraged to use appropriate tools strategically so that they can work toward a deep understanding of the formal algorithm.  Young learners can benefit greatly from the use of manipulatives, drawing, and the use of number lines to help them to understand subtraction. For example, young learners might start with base-10 blocks and represent the problem as follows. They will see that they need to “take away” 316 from the starting value of 427. Using the blocks, they can model 427 and then take away the needed amount (316) to see the result of 111. Later, as shown, students might draw out the blocks as they transition from the concrete manipulatives to paper and pencil to mental math. To arrive at the goal of fluent mental math computations, students need to have had developed mental images of what they are doing mentally! Otherwise, there is nothing mentally to connect to and the goal of fluency cannot be achieved.

1. Base-10 blocks: The “1” block is just a single tile. The “10” block contains ten “1” blocks stacked vertically. The “100” block consists of ten “10” blocks stacked horizontally.

2. Model the quantity 427.

 3. Take away 316 from 427 (represented by the red X’s).

4. Write the value of the remaining blocks.

 

With time and repeated reasoning (not repeated mimicking or doing without thinking), students will transition from using the blocks to sketching the drawings to just doing the computation in “under 5 seconds”.

Note: This example did not require “borrowing” (aka regrouping). The base-10 blocks and/or drawings can help students to develop a deep understanding of this as well. Maybe this can be part of the next post!

Misconception #3: Not all problems require thinking about subtraction as “take away”. Subtraction can also be thought about as an additive comparison. The common core helps students to develop strong problem solving strategies and this is a great example. Suppose the problem was something like:

Samantha had $427 and spent $316. How much money does she have left? This problem is clearly a situation where $316 are being “taken away” from $427.

What if the problem was something like:

Samantha has $427 and her sister Gloria has $316. How much more money does Samantha have than Gloria? This is not a “take away” situation. This is a comparison situation. We might think about this situation by counting up from $316 until reaching $427. Or, we might count down from $427 until reaching $316. With young learners, a number line can help them to visualize this strategy.  As students become more and more sophisticated with their thinking, they might count down by 100’s, 10’s, and/or 1’s as needed. If a student were to verbalize their thinking, they might say, “start with 427 and count down by 100 to 327…count down another 100 to 227…count down another 100 to 127. Then, count down 10 more to 117. Finally, count down 6 more…117, 116, 115, 114, 113, 112, 111.” Samantha has $111 more than Gloria.

I re-emphasize that we will not leave the learning at this place. Good teachers who are implementing the common core will continue to deepen student understanding by making connections to subtraction. Note that as we compare $427 and $316, we can argue that both quantities have at least $316. The difference (and that is why we call the result of subtraction the difference!) between the two quantities is the $111 additional that Samantha has!

Misconception #4: Some people might think that the status quo is fine with regards to teaching math. We should just “teach” students mathematics in ways that it has always been done. As a life long mathematics educator, I just can’t support this view. I currently teach at a community college where many students enter unprepared for college level mathematics. Internationally, the US scores poorly in mathematics in comparison to other nations. Students make decisions about college majors and careers based on programs of study that require the least amount of mathematics. Math anxiety is a real problem and is often caused when people try to mimic procedures that don’t make sense. When things don’t make sense, students struggle to succeed and have negative feelings toward such things. People complain that the cashiers at McDonald’s can’t make change.  This has been the case without common core! If people have a complaint about how the common core standards are organized, it would be wonderful to hear a better plan!

In summary, the common core standards absolutely do promote fluency (fast and efficient computations). This does not happen on its own but has to be developed! The common core, through the Standards for Mathematical Practices, provides students the opportunity to develop a deep, well-connected understanding of fundamental mathematics so that they can use mathematical tools and skills to solve problems.

Scott

Misunderstanding the Common Core

The following picture has been going around Facebook as an example of how crazy the new Common Core Standards must be:

The argument is that in the “old fashioned” way, we can get the answer in just a very few steps. In the “new” way, it take many more steps and is more confusing. This superficial view and example of the common core standards misses the point entirely. Please consider the context by which either method might arise in the thinking of a student.  For example, suppose the situation was that Ken had $32 and spent $12. Ken took away $12 from $32 and one might be thinking in the so called “old fashion” way. This is the “take away” model for subtraction. Suppose the situation was that Ken has $32 and Scott has $12. How much more money does Ken have than Scott? We are making a comparison (comparison model of subtraction). To make the comparison…to find the difference between how much Ken has and how much Scott has, one might start with Scott’s amount ($12) and add up to your amount: 8 more than $12 gets me to $20…another $12 gets me to $32…a total of $20 more. There are misconceptions that we are teaching new ways over old ways…not true! We are recognizing how one might think about the solution to a problem and that, depending on the situation, we might think in different ways.

People sometimes look at this example and make comments like, “no wonder our kids are confused when it comes to math!”

Actually, the issue is this: if the problem says (as in my second example) “how much more money does Ken have than Scott?” students see the word “more” and want to add 32 + 12! They are taught to look for “key words” like “more” which means to add. What I am saying is that we want students to think and make sense of the situation and solve the problem accordingly. My thinking in the “how much more” question might be to start with my $12 and add up to Ken’s $32. In the “Ken spent $12” question, I am thinking about subtraction because I am thinking about taking away $12 from the original $32. We are not showing new ways to subtract…we are solving problems in ways that might make sense.

By the way, in the given example, a young learner might count up to $32 from $12 in more or less sophisticated ways. In this case, it appears that that the student first counted up to $15 so that she could then count by 5’s (which may be more comfortable than counting by 8’s or 12’s). Once they counted up to $30, she only needed to count 2 more to get to $32 for a total of $20 more. This is great reasoning that respects that particular child’s thinking process!

For those that think that the common core is all about teaching “new” and confusing ways to “do math”, don’t worry…we are still teaching “old fashioned” subtraction! But, we are also teaching students to think, reason, make sense, solve problems, etc. You might consider the Common Core Standards for Mathematical Practices. This is the “core” of the Common Core:

1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.

Scott