Here we go again…another false statement about the “dumbing down” of American kids…about doing math in ways that seem foolish…about the “idiocy” of the Common Core Standards.
If you want to see the original post, go here: toprightnews.com/?p=3958
Most of what is discussed here has already been addressed in Parts I – IV. But I will use this post to highlight some of the issues and why I claim that folks like this (in this case, Jason DeWitt of Top Right News) are misrepresenting the Common Core Standards and that the root of the issue is their misunderstanding of the Common Core Standards.
Point #1 – The standards do NOT tell teachers/students how to do arithmetic
In the article, we see the following:
One student got tired of being dumbed-down by Common Core’s convoluted “standards” to do basic arithmetic.
“Standards” like how to add two numbers, which the student was told to do like THIS:
I challenge any reader to show me where in the Common Core Standards that students are told to “do basic arithmetic” in any specific way. Certainly, you will see standards that encourage students to make sense of mathematics…to understanding computational algorithms…to explain their thinking. Also, you will see standards that encourage computational fluency. What this is really an example of is how young learners might begin to make sense of the traditional algorithm for adding two numbers. Mathematics educators would NOT expect students to remain at this stage…rather, we expect students to develop computational fluency by thinking about the mathematics involved. Here is the example shown in this article:
I must be crystal clear…this is not an example of how students HAVE TO do this computation…this is an example of how a student MIGHT THINK about the computation.
Can we all agree that it is easier to do mental math that involve numbers like 20, 30, or 40? So a student might think…”26 is four less than 30…so let’s think about using the number 30.” Since we are adding 4 to 26, we would have to subtract 4 from 17 in order to get an accurate result for the final sum. Instead of thinking about 26 + 17, think about 30 + 13…which is 43.
I challenge you to ask 10 adults how they might think about 26 + 17 mentally…some will do this method! Some will imagine the algorithm in their minds eye (6 + 7 = 13…carry the one…2 + 1 + 1 + 4…so 43). Some might take 17 up to 20 by adding 3…which means we would have to subtract 3 from 26 to get 23…therefore, 26+17 is the same as 23+20 = 43. Can we all agree that 23 + 20…or 30 + 13… are easier to do mentally than 26 + 17?
Point #2 – There is no such thing as “the common core way”
In the article, another example is given and the following statement is made:
So when he was given his next basic arithmetic assignment, to find the difference between 180 and 158 (180-158), this 5th grade student just did it his own way — the right way –
Exactly…the student “did it his own way…” That’s what we want! We want students to make sense of the mathematics involved in these computations and to develop a fluent and efficient way to compute. While the article makes this statement as a way to diss the common core…I argue that this is exactly what the common core would encourage! As long as “his own way” was a way that makes sense to him and to others.
Ok…ok..I get it…the point of the article is that the student “stuck it to the common core man” by explaining how he found the answer…using one word…MATH! How cute…how clever…
Please…common core bashers…explain to me…what is so wrong with asking a student to explain his/her thinking? My hunch is this…you can’t do it so you don’t want your kids to do it. That is, you are uncomfortable explain your thinking so why should your kids have to explain their thinking? And if your kids are asked to explain their thinking and you don’t know how to help them do it, then there is something wrong with the assignment/teacher/standards/textbook/test/whatever.
Hmmm…mathematical thinking…not mathematical doing…mathematical thinking…
Kaye Stacey writes about mathematical thinking this way
The ability to think mathematically and to use mathematical thinking to solve problems is an important goal of schooling. In this respect, mathematical thinking will support science, technology, economic life and development in an economy. Increasingly, governments are recognising that economic well-being in a country is underpinned by strong levels of what has come to be called ‘mathematical literacy’ (PISA, 2006) in the population.
Do we want students who can “use mathematical thinking to solve problems”? Do we want to encourage our kids to engage in mathematical thinking to support “science, technology, economic life…”? Then we must stop showing kids how to do mindless procedures and instead help them to develop the mathematical thinking that leads to procedural fluency. Procedural fluency does not just happen magically. It is developed…and can be developed in such a way as to also develop and support mathematical thinking.
Think about the last time you had to divide two fractions…like 7/8 divided by 3/4.
First…this probably last occurred on your 7th grade final exam! Just kidding…but think about it…would you just “invert and multiply”? Is it important to understand the mathematics entailed in this computation? I say yes….
Scott
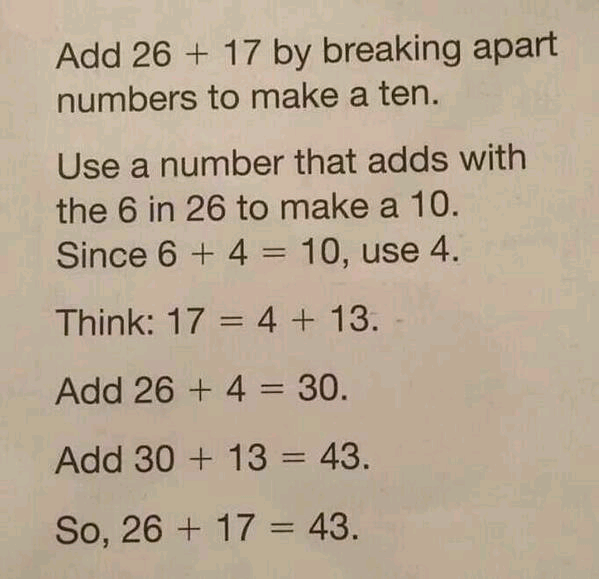
I agree with your primary point — that the common core doesn’t tell people to use ridiculous methods to solve problems. But I disagree with two other points that you make, one implied and one explicit:
1) You imply that because the common core doesn’t say that you should ridiculous methods to solve problems that people aren’t being instructed to do so. This is simply incorrect. Many students are being asked to use such methods or develop methods on their own that are inefficient and tedious. At our school kids may be shown a standard algorithm to do multiplication at some point, but by that time, many are so used to drawing 7 bugs with 8 legs each in order to find 7 * 8 that it becomes a hard habit to break.
2) Understanding the math isn’t always that important. One doesn’t have to understand WHY 7 * 8 = 56 in order to use this information in a useful way. One also doesn’t have to understand why “flip and multiply” works in order for it to be useful. Being able to explain algorithms isn’t doing math, and in some schools this is what it has become. As with many other disciplines, math consists of building a toolset that allow you to solve problems. Once you have tools in your belt, you don’t really need to be able to explain WHY the tools work in detail, you just need to be able to know WHEN to use the and HOW to use them. Does one have to know how a power drill works in order to know that it’s useful when you want to drive screws? (The answer is “no.”)
Doing rote problems without understanding the applicability of a technique is worthless. But wallowing in details that aren’t necessary to doing useful work also tends to bog down progress in practical applications. If a student wants to understand the WHY, a teacher should be able to explain in a way that a student can understand, but students can do an awful lot of math without knowing these things.
Thank you for your reply!
I have embedded my responses to your points in bold within your comments below:
I agree with your primary point — that the common core doesn’t tell people to use ridiculous methods to solve problems. But I disagree with two other points that you make, one implied and one explicit:
1) You imply that because the common core doesn’t say that you should ridiculous methods to solve problems that people aren’t being instructed to do so. This is simply incorrect. Many students are being asked to use such methods or develop methods on their own that are inefficient and tedious. At our school kids may be shown a standard algorithm to do multiplication at some point, but by that time, many are so used to drawing 7 bugs with 8 legs each in order to find 7 * 8 that it becomes a hard habit to break.
First, the question must be asked, “By whom are students being asked to use ridiculous methods?” Their teachers? The curriculum? Whatever, this is not a common core issue.
You show your beliefs about teaching mathematics in this paragraph. You say, “At our school kids may be shown a standard algorithm…” In my thinking, students are shown algorithms. They are given tasks that ask them to move, in a logical progression, from drawing bugs and legs to using efficient algorithms. In fact, this is what the common core proposes. Having written that statement, I don’t mean to say that common core somehow controls good teaching and learning! I should say that research on learning in mathematics proposes this progression! Students must work to make sense of multiplication by possibly first using manipulatives…then drawing bugs and legs…then using more abstract symbolism (numerals)…then efficient algorithms. The progression of tasks (with the support of a high quality teacher) will help students to move from more concrete representations to more abstract representations and helping the student to make the necessary cognitive connections between these representations.
2) Understanding the math isn’t always that important. One doesn’t have to understand WHY 7 * 8 = 56 in order to use this information in a useful way. One also doesn’t have to understand why “flip and multiply” works in order for it to be useful. Being able to explain algorithms isn’t doing math, and in some schools this is what it has become. As with many other disciplines, math consists of building a toolset that allow you to solve problems. Once you have tools in your belt, you don’t really need to be able to explain WHY the tools work in detail, you just need to be able to know WHEN to use the and HOW to use them. Does one have to know how a power drill works in order to know that it’s useful when you want to drive screws? (The answer is “no.”)
Are you saying that students shouldn’t be expected to understand why 7*8=56? Or, just that one need not ALWAYS have to understand why every time they need to multiply 7*8? If the former, think about this…we might as well tell kids stuff like & # @ = %. What meaning do these symbols have? The brain really struggles to memorize basic facts like this if they are just random symbols (from the eye of the student). Brain research suggests that students memorize more powerfully when the things they are memorizing are part of a well-connected network of understanding.
“Being able to explain algorithms isn’t doing math.” Now, we may just have to agree to disagree here…but I argue that explaining algorithms is EXACTLY what doing mathematics entails! Mathematics is about making arguments, justifying conclusions, making and testing conjectures. Your statements lead me to think that you think mathematics is all about following algorithms and procedures whether or not they make sense to the students. I disagree and think that the research literature on teaching and learning will support the notion that students are able to follow algorithms and procedures BETTER when they make sense…and we know that students show that they have made sense when they are able to explain the how’s and the why’s to others.
Doing rote problems without understanding the applicability of a technique is worthless. But wallowing in details that aren’t necessary to doing useful work also tends to bog down progress in practical applications. If a student wants to understand the WHY, a teacher should be able to explain in a way that a student can understand, but students can do an awful lot of math without knowing these things.
Agreed! But I am not proposing that one “wallows” in the details every time we engage in the computational side of math. I believe in the idea of knowledge packages (read Liping Ma). I might know a lot about subtracting whole numbers but when it comes to needing to compute quickly, I do it and move on! But if asked, I could also explain the details behind the mathematics. I want to live in a society where people have such knowledge about basic mathematical ideas. When people complain that kids at McDonalds can’t make change, it is not because they have just not practiced meaningless (from the eyes of the students) procedures enough! It is because they lack a profound understanding of fundamental mathematics (again…check out Liping Ma).