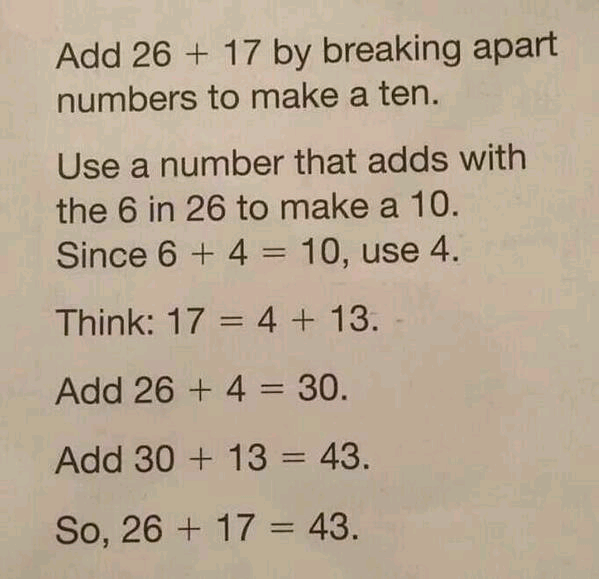Misunderstanding the Common Core Part X

Here we go again! I just saw the following on Facebook:

What was wrong with the old way? Before I answer…IT”S NOT THE OLD WAY! It’s just A WAY! If you want to read much about misunderstanding the common core, consider the other posts with a title “Misunderstanding the Common Core Parts I-IX”. I will reiterate, recap, and re-explain for anyone new to this blog.

When we subtract as shown at the bottom of the image, 568 – 293 = 275, there is a lot going on in terms of understanding the algorithm. Understanding the algorithm is what allows us to be efficient and accurate in computing by hand. Which brings us to an interesting issue: most people would use a calculator to do this!

Suppose you were going to attempt to compute 568 – 293 in your head. Or, suppose you were estimating. You might start with 568 – 200 = 368 just to get the thinking started. You might estimate/round 293 and say it is nearly 300 so 568 – 300 is about 268. Here’s my point…the most important digits are the digits in the 100’s place not the 1’s place! It is much more natural to start with the 100’s place than with the 1’s place as is traditionally done.

Let’s get back to it…once we think 568 – 200 = 368, the next thing to think about is the 10’s place. Let’s subtract 90 more. 368 – 90….hmmmmm…well…368 – 60 would be 308….hmmm…10 more…308 – 10 = 298….hmmm…20 more…298 – 20 = 278. It’s hard to do in writing but what I am trying to convey is that when people think about computations mentally, they might first focus on easier computations…subtracting 60, then 10, then 20 is much easier to do in my head that subtraction all 90 all at once.

So, we have subtracted 568 – 290 so far and have arrived at 278. Now subtract 3 more…278 – 3 = 275. There  you go! 568 – 293 = 275!

It would happen much faster in my head in reality than it seems when you read through everything that is happening in my head. Here it is in one, smaller space:

568 – 293….well, 568-200 = 368….now 368 – 90 is 368 – 60 = 308 and 308 – 10 = 298 and 298-20 = 278. Finally, 278 – 3 = 275…done…and fast!

What’s wrong with the old way? Nothing! What’s wrong with thinking, focusing on place value, mental math, understanding algorithms, and number sense? Nothing!

Here is the bottom line to me when it comes to this particular image. When we try to explain our thinking and show all the details of doing a simple subtraction problem, it might look convoluted and confusing. When we really think about how things work and try to understand the structure of the algorithm, it can make perfect sense!

One more thought…at the bottom of the image, we see this…

People look and say…wow, look how easy that was compared to that new, crazy math that my kids are coming home with! Yea, right! There is so much missing that many 3rd graders would not understand!

Likely, people would start on the right and find that 8 – 3 = 5. Fine.

Next, people would look at the 10’s place…6 – 9…hmmm…you can’t take 9 from 6! Sometimes kids see this and their brains tell them to think about 9 – 6 and they put 3 in the 10’s place! But we know, you have to “borrow” from the 100’s place and actually subtract 16 – 9 = 7 (note…I am ignoring place value here since that is the traditional thing to do).

Finally, move to the 100’s place. Remember we borrowed 1 (ignoring place value and meaning) from the 5 to make it 4. So, 4 – 2 = 2 so put a 2 in the 100’s place.

There is so much going on here that a 3rd grader has to figure out. The creator of this image chooses to omit it in order to present a stark contrast from “the old way” to the “common core way.”

Making sense of mathematics (in this case 3rd grade subtraction) as I have tried to do in this blog post is not crazy…it is not new….it is just MATH!*

 

*Credit to Dr. Ted Coe!

 

Misunderstanding the Common Core Part IX

“Five percent of the people think;
ten percent of the people think they think;
and the other eighty-five percent would rather die than think.”

-Thomas Edison

I don’t know exactly what Edison meant by this or how he determined the percentages, but the message, to me, is this: thinking is not what people do well!

On a recent Sunday news show, Texas governor Greg Abbott claims that the Common Core State Standards are bad because “it takes a teacher more than a minute to teach a student how to learn that 9+6=15”. He is referencing this video. Check it out.

Let’s think about this. How is this an argument against Common Core?

Is teaching a student how to think about 9+6 = 15 a bad thing? There is a difference between just doing 9+6 and thinking about 9+6. The Common Core Standards clearly have an emphasis on procedural fluency. Students should be able to determine that 9+6=15 quickly. But, how will such fluency happen? It will happen when students have a way of thinking about 9+6. Because it takes a minute to explain this thinking does not mean that it will take a student a minute to compute! Furthermore, the expectation is to push mental math…a good thing! For a student to flexibly be able to see 9+6 as equivalent to 10+5 is very good!

Governor Abbott does not have the opportunity to explain how he believes students should be taught that 9+6=15, but I will make a conjecture that he will argue that students should just memorize it. And in saying this, what would he mean by “just memorize it”? Perhaps something like this (and I embellish):

Teacher: “OK Johnny, this shape right here (9) is called the number 9 and this shape right here (6) which kind of looks like an upside-down 9 is called the number 6. And when you put this symbol in between this (9) and this (6) the answer is two shapes…a 1 which sits right next to a 5. So 9 + 6 = 15”

Johnny: “But why?”

Teacher: “Don’t ask why…just memorize it. Let me get the flashcards.”

We might as well do something like this:

Teacher: “OK Johnny, let me tell you something that I want you to memorize. If you take purple and add dog the answer is banana.

Johnny: “But why?”

Teacher: “Don’t ask why…just memorize it. Let me get the flashcards.”

The teacher in the video is just unpacking the mathematical thinking necessary for a student to make sense of what 9+6=15 means and how this fact might be memorized in a meaningful way. Certainly, we expect students to be able to respond to 9+6 in just a few seconds. This memorized fact will be retained when the mathematical reasoning and thinking, done by the student, allows the student to make meaning and make sense of the computation.

And by the way…this kind of thinking, to allow students to memorize basic math facts, has been around long before the Common Core Standards! This is not a Common Core thing…this is just good teaching.

Diane Briars, president of the National Council of Teachers of Mathematics, says this about the issue: “Teachers have used techniques like splitting a number into parts of 10 for addition–rather than straight memorization–since the 1950s at least, and the research showing its benefits goes back to the 1920s. It has long been best practice for early childhood math.”

I encourage everyone…please read the Common Core Standards and understand their purpose. Then, if you want to debate the issue of the federal government offering federal money tied to the implementation of these standards, great! If you want to debate standardized testing, its cost, its taking instructional time, its impact on the mental health of students, teachers, and parents, great! But please…do not conflate these issues. Standards are standards…teaching is teaching…curriculum is curriculum…testing is testing. My experience is, when people actually consider the Standards, the issue is not the Standards! When they see that students are expected to become effective problem solvers, mathematical thinkers, and fluent in computations, most agree that the Standards are not a problem.

When people try to show that the Standards (not the role of the feds, not standardized testing, etc.) are bad, it is clear that they are not really thinking…

 

 

Misunderstanding the Common Core Part VII

Here is the latest (for me) bashing of the common core standards:

http://toprightnews.com/?p=6326

Again, the subject of the bashing is subtraction…I find it interesting that subtraction seems to be taking the biggest hit when it comes to common core bashing!

The blogger says, “Here is the insane “method” they came up with to utterly confuse 4th graders about subtraction:”

Insane? Utterly confuse? I think not!

Consider this: Albert Einstein was born in 1879 and died in 1955. How old was he when he died? Think about it…then pay attention to how you thought about it…

Many adults think about this situation like this:

• Starting with 1879, it takes 21 years to get to 1900.
• Then, another 55 years takes us to 1955.
• So, Einstein was 21 + 55 = 76 years old (or would have turned 76) in 1955.

This is the “counting up method” described in the textbook! This method seems SANE and UTTERLY sensible to me!

As I have explained in other posts (Part I, Part II, Part III, Part IV, Part V, Part VI), the main issue is how one thinks about subtraction. If one only thinks about subtraction as “take away” then their understanding is incomplete. We can also think about subtraction as a comparison…which is really what is happening here. We are comparing 1955 to 1879 to see how many years have elapsed. Furthermore, think about the method (yes, it is a method!) described early…first add 21 years…then add 55 years…and compare that method to the standard subtraction algorithm from a “take away” perspective.

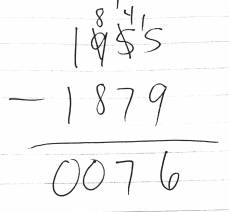With the double borrowing, mistakes can be made. In addition, I am a fan of mental math…it can absolutely be a helpful and healthy thing to keep track of quantities mentally!

The goal…and who can really argue this…is for students to become fluent, flexible, and efficient with computations.

• Fluent in a way similar to becoming fluent in a foreign language…comfort, ease, speed, and confidence are all hallmarks of fluency.
• Flexible in the sense that a student will use an algorithm if necessary, use a counting up strategy if possible, or other strategies learned in school.
• Efficient in the sense that a student will choose a strategy that is appropriate for the task at hand. For example, in the Einstein example, I argue that the counting up strategy is more efficient than the traditional algorithm…at least for those who have been trained to think that way!

Scott

Misunderstanding the Common Core Part V

Here we go again…another false statement about the “dumbing down” of American kids…about doing math in ways that seem foolish…about the “idiocy” of the Common Core Standards.

If you want to see the original post, go here: toprightnews.com/?p=3958

Most of what is discussed here has already been addressed in Parts I – IV. But I will use this post to highlight some of the issues and why I claim that folks like this (in this case, Jason DeWitt of Top Right News) are misrepresenting the Common Core Standards and that the root of the issue is their misunderstanding of the Common Core Standards.

Point #1 – The standards do NOT tell teachers/students how to do arithmetic

In the article, we see the following:

One student got tired of being dumbed-down by Common Core’s convoluted “standards” to do basic arithmetic.

“Standards” like how to add two numbers, which the student was told to do like THIS:

I challenge any reader to show me where in the Common Core Standards that students are told to “do basic arithmetic” in any specific way. Certainly, you will see standards that encourage students to make sense of mathematics…to understanding computational algorithms…to explain their thinking. Also, you will see standards that encourage computational fluency. What this is really an example of is how young learners might begin to make sense of the traditional algorithm for adding two numbers. Mathematics educators would NOT expect students to remain at this stage…rather, we expect students to develop computational fluency by thinking about the mathematics involved. Here is the example shown in this article:

I must be crystal clear…this is not an example of how students HAVE TO do this computation…this is an example of how a student MIGHT THINK about the computation.

Can we all agree that it is easier to do mental math that involve numbers like 20, 30, or 40? So a student might think…”26 is four less than 30…so let’s think about using the number 30.” Since  we are adding 4 to 26, we would have to subtract 4 from 17 in order to get an accurate result for the final sum. Instead of thinking about 26 + 17, think about 30 + 13…which is 43.

I challenge you to ask 10 adults how they might think about 26 + 17 mentally…some will do this method! Some will imagine the algorithm in their minds eye (6 + 7 = 13…carry the one…2 + 1 + 1 + 4…so 43). Some might take 17 up to 20 by adding 3…which means we would have to subtract 3 from 26 to get 23…therefore, 26+17 is the same as 23+20 = 43. Can we all agree that 23 + 20…or 30 + 13… are easier to do mentally than 26 + 17?

Point #2 – There is no such thing as “the common core way”

In the article, another example is given and the following statement is made:

So when he was given his next basic arithmetic assignment, to find the difference between 180 and 158 (180-158), this 5th grade student just did it his own way — the right way – 

Exactly…the student “did it his own way…” That’s what we want! We want students to make sense of the mathematics involved in these computations and to develop a fluent and efficient way to compute. While the article makes this statement as a way to diss the common core…I argue that this is exactly what the common core would encourage! As long as “his own way” was a way that makes sense to him and to others.

Ok…ok..I get it…the point of the article is that the student “stuck it to the common core man” by explaining how he found the answer…using one word…MATH! How cute…how clever…

Please…common core bashers…explain to me…what is so wrong with asking a student to explain his/her thinking? My hunch is this…you can’t do it so you don’t want your kids to do it. That is, you are uncomfortable explain your thinking so why should your kids have to explain their thinking? And if your kids are asked to explain their thinking and you don’t know how to help them do it, then there is something wrong with the assignment/teacher/standards/textbook/test/whatever.

Hmmm…mathematical thinking…not mathematical doing…mathematical thinking…

Kaye Stacey writes about mathematical thinking this way

The ability to think mathematically and to use mathematical thinking to solve problems is an important goal of schooling. In this respect, mathematical thinking will support science, technology, economic life and development in an economy. Increasingly, governments are recognising that economic well-being in a country is underpinned by strong levels of what has come to be called ‘mathematical literacy’ (PISA, 2006) in the population. 

Do we want students who can “use mathematical thinking to solve problems”? Do we want to encourage our kids to engage in mathematical thinking to support “science, technology, economic life…”? Then we must stop showing kids how to do mindless procedures and instead help them to develop the mathematical thinking that leads to procedural fluency. Procedural fluency does not just happen magically. It is developed…and can be developed in such a way as to also develop and support mathematical thinking.

Think about the last time you had to divide two fractions…like 7/8 divided by 3/4.

First…this probably last occurred on your 7th grade final exam! Just kidding…but think about it…would you just “invert and multiply”? Is it important to understand the mathematics entailed in this computation? I say yes….

Scott

Misunderstanding the Common Core Part IV

I was recently made aware of the following video bashing common core math…

There are many reasons why they video represents a misunderstanding of common core math. Let’s start with some possible mathematical understandings represented in the video. The host, Caleb Bonham, shows people how common core purportedly wants students to calculate 134 – 52.

Right away, Mr. Bonham says “four minus 2…2, 4 minus 5…carry the one…” What? Carry the one? Imagine a student learning (and by learning I mean mimicking) this algorithm for the very first time.  If Mr. Bonham was the teacher, he would say, “alright kids…4 minus 5…carry the one…” What is the mathematics that supports this? What does it mean to “carry the one”? Why is he carrying the one? Where is this one coming from? Is it one because somehow 4 minus 5 involves the number one?

When showing the so called “common core way” of computing the difference, he says, “you can’t just do it like this (the traditional algorithm)” and he proceeds to show what he believes is the common core way in a very mocking way. What he fails to realize is that this is not “the common core way.” What he is showing is just one way to make sense of the traditional algorithm! If students are thinking (note…this is what we want students to do…not just “carry the one” without any understanding or reasoning) about subtraction as taking away one quantity from another and if students are learning about the idea of regrouping (aka borrowing) for the first time, then the representation he shows makes a lot of sense! The dots provide a visual representation of the computations in the traditional algorithm…very useful for a young learner who is trying to make sense of the ideas.

The student starts by subtracting (taking away) 2 of the dots from the ones place. Great! The student moves to the tens place and needs to take away 5 tens…but only has 4 tens…what should they do? In the traditional algorithm shown by Mr. Bonham, he proposes that the student just crosses off the one in the hundreds place and “carries” it to the tens place. He says, “thirteen minus 5 is eight.” While this produces the right answer in the end, the articulation of the mathematics is wrong (I will explain below). The dot method he shows explains the mathematics.

When the student comes across the dilemma of taking away 5 tens from 4 tens (in reality, taking 50 away from 40), the solution is to look to the hundreds place and exchange one-hundred for 10 tens. The ten dots (each representing a quantity of 10) is placed in the tens column. Think about it…13 tens is one-hundred and thirty which is equivalent to one 100 and 3 tens. But now, we can take away 5 tens (50) from 13 tens (13) leaving 8 tens (80). So, when Mr. Bonham “carries the one”, he is actually exchanging one 100 for ten 10’s so that the subtraction (as take away) is possible. Nice!

Mr. Bonham makes a mathematical error when he asks the gentleman, “how many 10’s in 134?” and they respond “3” and make “three little dots.”

Let’s think about this…something that the common core wants students to learn to do…to make sense, reason, etc. How many tens are in ONE HUNDRED AND THIRTY FOUR? Only 3 (I think the man on the right says 30!)? What? I would say that three tens make 30! That’s not even close to ONE HUNDRED AND THIRTY FOUR! Let’s think about that again…how many tens are there in ONE HUNDRED AND THIRTY FOUR? If we had 10 tens, that would be 100…13 tens is 130…so there are 13 tens in ONE HUNDRED AND THIRTY FOUR…13 tens and 4 ones. Suppose a student was thinking (not just trying to mimic an algorithm) about both numbers in this way. That is, we have 13 tens and 4 ones…take away 5 tens and 2 ones…13 tens take away 5 tens is 8 tens (80) and 4 ones take away 2 ones is 2…so the answer is 82! No algorithm needed! Now that is efficient! If efficiency is what we are after, then let’s do it my way!

Mr. Bonham likes to make the point that doing math is all about being efficient. Let’s compare his method with mine…

On the left is the traditional method shown by Mr. Bonham:

1. Think…what’s 4 minus 2? Write down 2
2. Think…what’s 3 minus 5? Can’t do it so carry the one (whatever that means)
3. Think…what’s 13 minus 5? Write down 8 (note…it is really 13 tens (130) minus 5 tens (50)…not 13 minus 5.

On the right is the way I describe:

1. Think…what’s 13 tens minus 5 tens? Write down 8 in the tens place realizing that 130 minus 50 is 80.
2. Think…what’s 4 minus 2? Write down 2.

One less step…and much more understanding!

Now…here is the real bottom line in my opinion…Mr. Bonham makes a claim that there is the “efficient way” (according to him) and the “common core way”. That is just not true. The common core pushes for a balance between conceptual understanding (perhaps thinking about place value and understanding the mathematics behind carrying the one) and procedural fluency (computing answers quickly and accurately). It is absolutely false to believe that the common core is proposing some long, inefficient method to compute. But…how does one develop computational fluency? Young learners would need to do things like use manipulatives, draw dots, represent their thinking in a visual way, explain their thinking. Then…and only then…can a young learner possible move to using Mr. Bonham’s algorithm or perhaps even better (it IS more efficient) using the left-t0-right algorithm that I proposed above! Computational fluency…the “efficient way” does not just magically happen!

A challenge: download the common core math standards at http://www.corestandards.org/Math/. Search for the word “fluency” and see how often students are expected to demonstrate computational fluency! Or, continue to stick your head in the sand and listen to people like Mr. Bonham who probably have never even read the common core math standards!

Scott